一.第一印象dfs。

 dfs是一种常用于图和树的遍历算法，用于遍历所有节点。要掌握dfs，必须理解递归思想。dfs可以理解为一条黑色࿰的道路c;不能，回到，然后往下走。

二.dfs模板。

基本思路分析：个人认为重点是找到递归重复的部分，也就是说，在主题中找到重复需要执行的部分，然后是对递归出口的判断；然后回溯，剪枝，记忆搜索等优化。

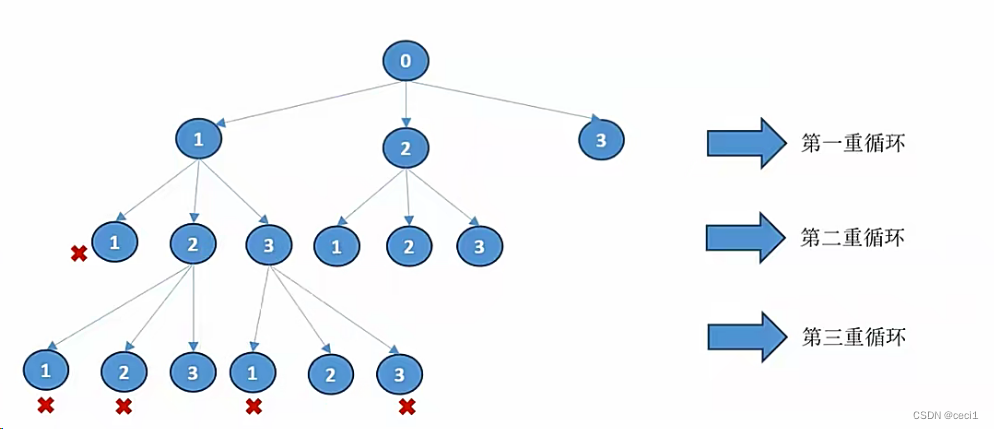
def dfs(depth):  #depth是当层的几个重循环，即深度  if depth==N:    #到达边界时，，即返回    return  #每个循环的枚举选择，也就是dfs递归。

三.优化。

3.1 回溯。

追溯就是在搜索试验过程中找到问题的解决方案，当发现不符合条件时，，回到，尝试其他路径。

强调这条路不通，另寻他路。先打标󿀌记录路径；然后下一层�回到上一层�清除标记。

3.1.1回溯法要求全排列。

def dfs(depth):#depth表示当前层数󿀌即已选择的数量  if depth==n:    #每次输出全排列    print(path)    return  for i in range(1,n+1):    #已标记    if vis[i]:      continue    #未标记    vis[i]=1    path.append(i)    #递归下一层    dfs(depth+1)    #回溯    #修改标记    vis[i]=0    #弹出这个数字    path.pop(-1)n=int(input()#标记数组，11标记，未标记vis=[0]*(n+#路径数组path#61;[]dfs(0)。

3.1.2.回溯法解决n皇后问题。

import osimport sysinput=sys.stdin.readline ans=0#思路：遍历每一行，即遍历的深度，然后在每列中选择合适的位置def dfs(x):  #出口  if x==n+1:    global ans    ans+=1  #第x层枚举每一列  for y in range(1,n+1):    #当前列和#xff0c;主对角线�标记了副对角线    if vis1[y] or visa[x+y] or visb[x-y+n]:      continue    #假如没有标记，先标记，再递到下一行(此时是合法点)    vis1[y] =visa[x+y] = visb[x-y+n]=True    #递归下一行    dfs(x+1)    #回到上一行�取消标记    vis1[y] =visa[x+y] = visb[x-y+n]=Falsen=int(input()#标记数组#vis1=[False]*(n+#主对角visa#61;[False]*(2*n+#副对角线visb=[False]*(2*n+1)#dfs(1)从1开始print(ans)。

3.2剪枝。

3.2剪枝。

可分为可行性剪枝和优化剪枝。可行剪枝：目前的状态与问题的意思不符c;而且以后所有的情况和题目都不符合，然后就可以剪枝了。最优化剪枝：在搜索过程中，目前的状态不如已经找到的最优解，也可以剪枝�不需要继续搜索。

3.2.解决数字王国军训排队的剪枝问题。

1.数字王国军训排队 - 蓝桥云课 (lanqiao.cn)。

• 思路：
• dfs搜索�每个学生都被分成每个小组。
• 可行剪枝：符合题目条件。

最佳剪枝：判断当前状态是否比ans差。

 。

import osimport sysinput=sys.stdin.readline#判断倍数关系#判断学生是否被放入当前的分组def check(now_group,y): #遍历当前组中的元素 for i in now_group: #是倍数关系 if i%y==0 or y%i==0: return False return Truedef dfs(depth): #depth表示，目前的第几名学生 #优化剪枝(因为队数不能超过学生人数) global ans if len(groups)>ans: return #递归出口 if depth==n: ans=min(ans,len(groups)) return #每个学生󿀌哪一组枚举？ for now_group in groups: #now_group表示目前的组 #可行性剪枝 if check(now_group,a[depth]): #放入 now_group.append(a[depth]) dfs(depth+1) now_group.pop() #直接再做一组 groups.append([a[depth]]) dfs(depth+1) groups.pop()n=int(input())a=list(map(int,input().split())#分的队数，相当于二维数组groups=[]ans=ndfs(0)print(ans)。

3.2.2 剪枝解决了特殊的多边形问题 。

3.2.2 剪枝解决了特殊的多边形问题 。

 。

 。

 。

import osimport sysinput=sys.stdin.readline#dfs要求所有n边形，边长乘积不超过100000def dfs(depth,last_val,tot,mul): #depth 第depth边󿀌last_val指的是边长，tot是边长之和，mul是边长的积累 #递归出口 if depth==n: #可行性剪枝 #满足n边形的基本定义 #最小n-1边之和大于第n边 tot-path[-1]>path[-1] if tot>2*path[-1]: #合法的n边形 ans[mul]+=1 return #枚举第depth条边的边长为i for i in range(last_val+1,100000): #最优化剪枝 #之前选择了depth数字󿼌乘积为mul #还有n-depth数字，每个数字都需要>i if mul*(i**(n-depth))<=100000: path.append(i) dfs(depth+1,i,tot+i,mul*i) path.pop() else: break t,n=map(int,input().split())#ans[i]n边形ans=[0]*100001path=[]dfs(0，0，0，1)#每次询问一个区间l，r,n边形的输出值是多少？[l,r]等价于ans的中#[l]+...+ans[r],需要求ANS前缀和fors i in range(100001): ans[i]+=ans[i-1]for _ in range(t): l,r=map(int,input().split()) print(ans[r]-ans[l-1])。

3.3记忆搜索。

3.3记忆搜索。

记录已经经历过的状态的信息，从而避免搜索实现同一状态重复遍历的方法。

#记忆化，fromm可以直接加导这个包 functools import lru_cache#将普通递归转化为记忆递归@lru_cache(maxsize=None)。

3.3.斐波那契数列的记忆解决方案。

 。

 。

#记忆化，fromm可以直接加导这个包 functools import lru_cache#将普通化转化为记忆化递归#64;lru_cache(maxsize=None)def f(x): if x==0 or x==1: return 1return f(x-1)+f(x-2)。 3.3.记忆化解决混沌之地。

用户登录。

 。

。

 。import sysinput=sys.stdin.readlinefrom functools import lru_cache@lru_cache(maxsize=None)def dfs(x,y,z): #x目前的横坐标󿼌y当前纵坐标�z是否使用背包 #出口 if x==C and y==D: return True #未到达出口，向四个方向行走 for dx,dy in (0，1)，(0，-(1，0)，(-1，0): xx,yy=dx+x,dy+y #边界判断 if xx<0 or xx>=n or yy<0 or yy>=m: continue #新位置的高度低于当前位置 if a[xx][yy]<a[x][y]: #直接走 if dfs(xx,yy,z): return True #新位置高于当前位置，差小于k，用背包 if a[xx][yy]-a[x][y]<k and z==False: if dfs(xx,yy,True): return True return False n,m,k=map(int,input().split())A,B,C,D=map(int,input().split())A,B,C,D=A-1,B-1,C-1,D-1a=[]for i in range(n): a.append(list(map(int,input().split())))if dfs(A,B,False): print("Yes")else: print("No")。 。 。

分享让更多人看到